下位蜃気楼シミュレーション (inferior mirage simulation)
2014年2月27日(木)〔初版〕:〔3月1日(土)改訂1〕 琵琶湖地域環境教育研究会 松井 一幸
上位蜃気楼に応用したページへ移動(2014.3.11記)
1.はじめに
蜃気楼(mirage)は、場所による大気の屈折率の違いからくる光の経路の変化によるもので、通常水平線付近に見られます。
実際の像の下側にできるものを下位蜃気楼(inferior mirage)、上側にできるものを上位蜃気楼(superior mirage)と呼んでいます。
上位蜃気楼は、4月から7月の暖かい時に偶にしか現れない蜃気楼です。このため、春の蜃気楼と呼ぶ人もいます。
下位蜃気楼はひんやりした日や冷え込む日に1年を通じてよく現れる蜃気楼です。冬の蜃気楼と呼ぶ人がいますが、冬に顕著に現れる機会が多いだけで、適した呼び方とは言えないと思います。
上位蜃気楼は、湖面近くの大気の上層部が下層部よりも暖かい時(上暖下冷)に起こります。
逆に、上層部に比べて下層大気の方が暖かい時(上冷下暖)には、下位蜃気楼が発生します。
蜃気楼が起きていない通常の景色は、実景と呼ばれています。
上位蜃気楼は、対象物が静止していても時々刻々変化するのに対して、下位蜃気楼は対象物が静止していると殆ど変化しない蜃気楼になります。
上位蜃気楼の時(上暖下冷)は大気が不安定であるのに対して、下位蜃気楼の時(上冷下暖)は安定で、長時間持続する傾向にあります。
下位蜃気楼になると、琵琶湖に浮かぶ島や対岸の林や家々は浮島現象が現れます。琵琶湖大橋は円盤や凸レンズ型になります。
ここでは、下位蜃気楼の仕組みを明らかにし、シミュレーションを行うことにします。
2.地球の形状と湖面方程式
下位蜃気楼シミュレーションを行う時には、地球が球体(正確には西洋梨型)であることからくる琵琶湖の湖面も球面であることを考慮する必要があります。
図-1に示すように、球面の効果は小さくはなく、実景の時にも水平線上の向こうに隠れて見えない沈んだ部分があることになります。
上位蜃気楼の時にはこの隠れた部分が顔を出す時がありますが、下位蜃気楼の場合には通常この部分が顔を出すことはありません。
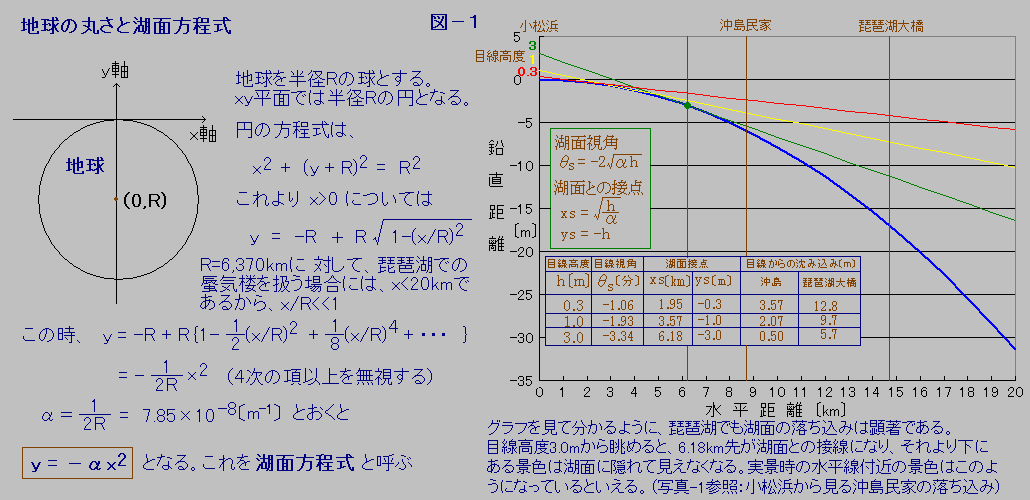
写真-1に、大津市北小松小松浜から眺めた8.7km離れた沖島民家の様子を示します。3枚の写真がありますが、目線の高さをおおよそ3m、1.5m、0.3mと変化させたものです。

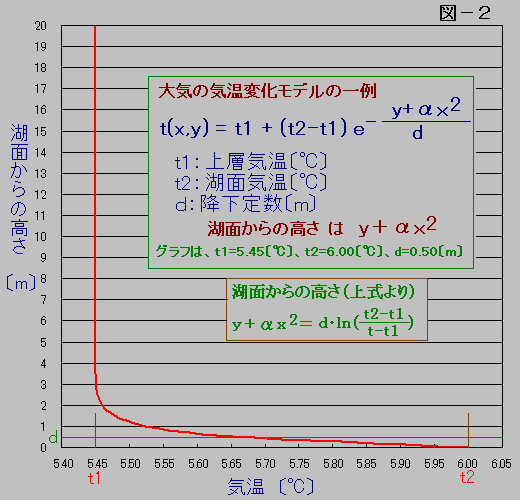
3.大気の気温
蜃気楼をシミュレーションする場合には、大気の湖面近くの気温の分布を知ることが必要になってきます。
ここでは、以下のような式で気温が変化するモデルを用いて単純化して考えることにします。
t(x,y) = t1 + (t2 - t1)exp{-(y+αx^2)/d) ここに、expは自然対数
t1〔℃〕は上層の気温。t2〔℃〕は湖面付近の気温です。下位蜃気楼は、t1〔℃〕< t2〔℃〕の場合に起こります。
(y+αx^2)〔m〕は湖面からの高さで、地球の丸さを考慮しています。
d〔m〕は、湖面から指数関数的に降下する気温差(t2-t1)が1/e(eはexpと同じ)になる距離で、ここでは降下定数と呼ぶことにします。
ここでは、気温は湖面からの高さのみで決まり、横方向には一様であるとしています。
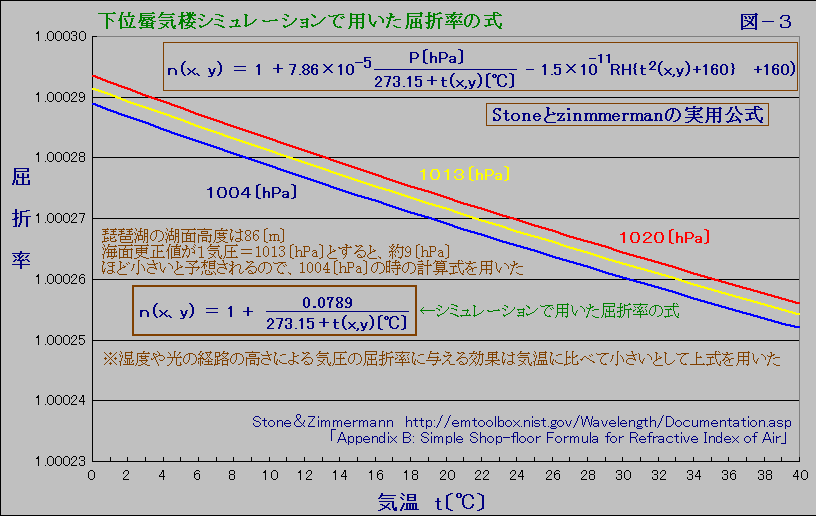
4.大気の屈折率(Refractive Index of Air)
蜃気楼のシミュレーションに重要なのは、大気の屈折率です。真空中の光速をC〔m/s〕とすると、大気中の光速V〔m/s〕は、V=C/nで与えられます。
ここにnは大気の屈折率で、気温、気圧、湿度、波長等に関係します。
Stone&Zimmermannの文献の「Appendix B: Simple Shop-floor Formula for Refractive Index of Air」には、簡易で実用的な式が報告されています。
ここでは、この実用的な式にP=1004〔hPa〕を用いたものを使います。
琵琶湖の湖面は平均海水面よりも約86m高い所にあるので、海面更正をすると1気圧の1013hPa程度になるように決めました。
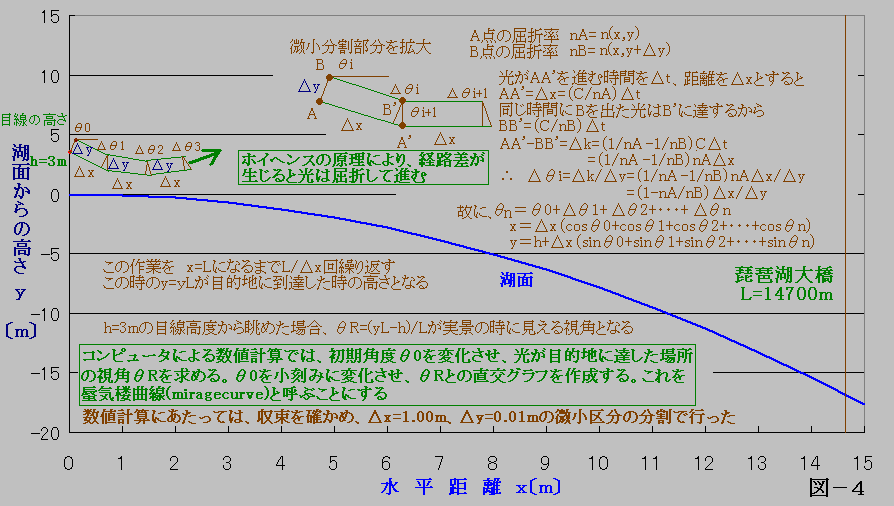
5.ホイヘンスの原理による光の経路の計算
湖面から上層へ向かって気温が低下する環境においては、大気の屈折率は湖面近くの方が小さく、従って上層よりも光速が早くなります。
我々は対象物から来る光を見ているのですが、光の経路を調べる場合は、光の進路の可逆性を利用して、目線から対象物へ向かう経路を考える方が計算し易くなります。
yと(y+Δy)の2点から出る2つの光を考えると、高さの差はΔyと極く小さいのですが、Δx進む間に移動距離の差が出てきます。
この僅かな差が、ホイヘンスの原理により光の経路をΔθ変えることになります。
図-4に説明しているように、Δθi={1-n(xi,yi+Δy)/n(xi,yi)}Δx/Δy
となり、この変化を繰り返しながら対象物へと進んでいきます。
屈折率n(x,y)の中にt(x,y)が含まれており、光の進路は複雑に思えますが、コンピュータは数値計算が得意なので容易にやり遂げてくれます。
i番目の角度、位置は、以下のようになります。
角度 θi=θ0+Δθ1+Δθ2+・・・+Δθi=θi-1+Δθi
x座標 xi=Δx(cosθ0 + cosθ1 +・・・+ cosθi-1)
y座標 yi=h + Δx(sinθ0 + sinθ1 +・・・+sinθi-1)
Δx、Δyをいくらの微小区間にするかという問題がありますが、計算の精度の問題と一定値へ収束するかという問題が生じます。
琵琶湖大橋まで14.7kmですから、Δx=1.00mにすると、目的地に達するまでに14,700回の計算をすることになります。
Δx=0.01mにとり、147万回の計算を行うと、手持ちのパソコンは2分余りかかり計算を終えましたが、yLの値には殆ど差はみられませんでした。
Δyは0.01mにとりました。計算は倍精度で行いましたが、あまり小さいと屈折率の差がなくなるのでこれくらいが適当と思われます。
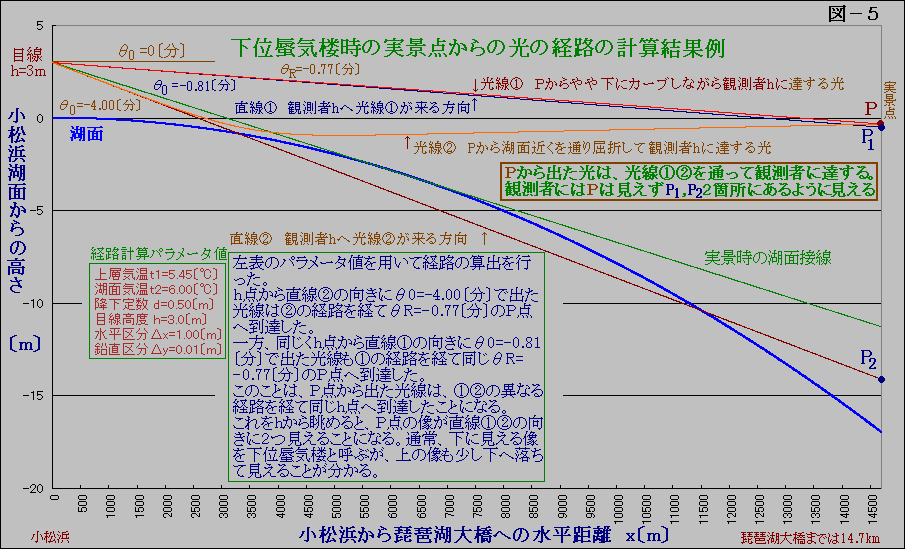
6.光の経路の計算結果例
実際の観察写真の説明ができるようにするため、観測点は大津市北小松小松浜湖面からの高さh=3.0mの地点とし、対象物はL=14.7km前方にある琵琶湖大橋としました。
前述の方法により、図-5中に示すパラメータ値を用いて光の経路計算を行いました。
目線高度h=3.0mの地点から、θ0=-4.00分で光を出発させると、湖面近くで強く経路がが上向きに曲げられてP点に到達しました。
角度を変化させて行くと、θ0=-0.82分でもL=14.7km前方では同じ高さのP点に到達しました。
これは、P点から出た光は、2手に分かれ、(1)光線①の経路を進み、観測点hへは直線①から来たように見える光と、(2)光線②の経路を進み、観測点hへは直線②から来たように見える光となって観察者に到達することになります。
これは、下位蜃気楼が起きる場合の上の像と下の像に対応していることにつながって行くのです。
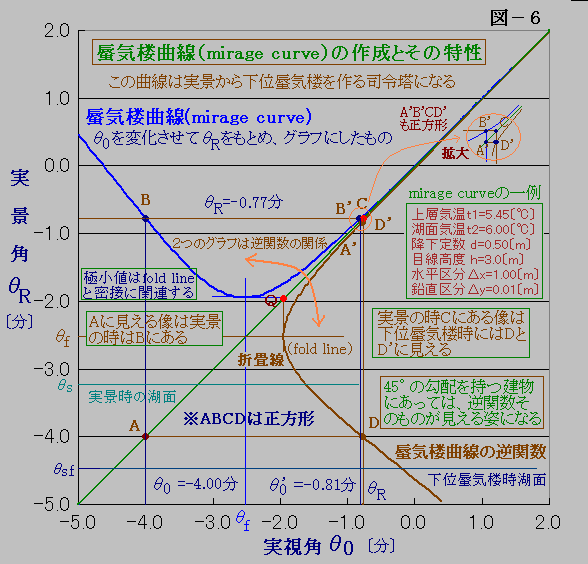
7.蜃気楼曲線(mirage curve)の作成とその特性
蜃気楼曲線(mirage curve)は、筆者がここで名付ける呼び名です。蜃気楼の専門書には似たような概念がすでに別の言葉で存在するかも知れません。
筆者には、実景から下位蜃気楼画像を作成する司令塔となる図に思えますので、作り方や読み取るべきことを分かりやすく伝えたいと思います。
蜃気楼曲線(mirage curve)と呼ぶ青色の曲線は、次のようにして作ります。
<蜃気楼曲線(mirage curve)図の作り方>
(1)θ0(観測点目線視角)を-5.00分に設定し、t1,t2,dのパラメータ値を設定し、「5.ホイヘンスの原理による光の経路の計算」で述べた処方に則り、L=14.7km先に到達した際の高度y座標の位置yLを計算します。
(2)θRは、実景時にyLにある物体の目線角度です。θR=(h-yL)/L〔rad〕=(h-yL)/L・180・60/3.1416〔分〕となります。
(3)θ0を-5.00分から0.05分刻みに2.00分まで変化させ、その時々のθRを計算します。そして、θ0を横軸に、θRを縦軸にプロットすると、求める蜃気楼曲線(mirage curve:青色)が得られます。
(4)蜃気楼曲線(mirage curve)を描いた時に、45°の傾きを持つ緑色の直線に対して対称なグラフ(茶色)を作成します。
これは数学的には蜃気楼曲線(mirage curve)の逆関数です。現実に見る蜃気楼との関係を捉えやすいグラフで、蜃気楼曲線(mirage curve:青色)の(横座標,縦座標)値を(縦座標,横座標)値としてプロットすると得られます。
<蜃気楼曲線(mirage curve)図の読み取り方>
蜃気楼曲線(mirage curve)の理解はやや複雑ですが、正しく理解できると本当に役に立つグラフになります。
(1)下位蜃気楼が見えている時の対象物の実視角をθ0=4.00分とします。図中ではAがこれに相当します。
(2)下位蜃気楼時にはA点に見える対象物が実景の時はどの角度に見えるかは、光の経路計算から蜃気楼曲線(mirage curve)との交点Bになります。
(3)実視角θ0を小さくしていくとθRは下がっていきますが、蜃気楼曲線(mirage curve)に極小値θfが現れます。(注:t1,t2,dの条件によっては単調関数で極小値が現れないこともあります)
これは、下位蜃気楼に特有の折畳線(fold line または vanishing line)が存在することを物語っています。
(4)さらにθ0を小さくしていくとθRは上昇に転じ、θ0'のA'で、点と同じ値θRを持つB'が現れます。
A'は下位蜃気楼時に上に現れる像で、Aは下に現れる像に対応します。
(5)緑色と青色の線の関係は、「下位蜃気楼時に緑色で見える視角にある対象物は、実景時には青色の位置まで上がった視角に見える」ことを示しています。
逆関数グラフの導入
(6)実際に視る下位蜃気楼のイメージと異なるので、蜃気楼曲線(mirage curve)の逆関数のグラフ作りを茶色で示します。
(7)緑色と茶色の線の関係は、「実景時に緑色で見える視角にある対象物は、下位蜃気楼時には茶色の位置まで下がった視角に見える」ことを示しています。
この関係は、茶色のグラフは普段目にする姿とよく似ているので下位蜃気楼に対する理解が深まります。
実際、45°の傾きを持つ斜面状の物体が下位蜃気楼を起こすと、このような下位蜃気楼曲線になります。
任意の形の物体の場合には、緑の直線上の点に対応する位置が、茶色のグラフ位置まで下がることになります。
(8)蜃気楼曲線(mirage curve)の極小値θfは、そのまま折畳線(fold line)の意味を持ちます。この視角θfを境に下には上下反転した蜃気楼が現れます。
(9)下位蜃気楼時の湖面角θsfは、光の経路計算で湖面にぶつかる最大角(絶対値は最小)で計算できます。実景時の湖面角θsと比べると、θs>θsfとなり、湖面は落ち込み観測者の近くへきます。
(10)グラフは、折畳線(fold line)近傍にくると、①落ち込みが激しくなること、②図中Qより下の物体は見えない、ことが分かります。
①は下位蜃気楼像が折畳線(fold line)近傍では、物体が丸みを帯びることを示します。
(11)折畳線(fold line)の上下の像の高さの幅に違いがあるかについては、曲線がほぼ上下対称になっているので、大きな違いはないように思われます。
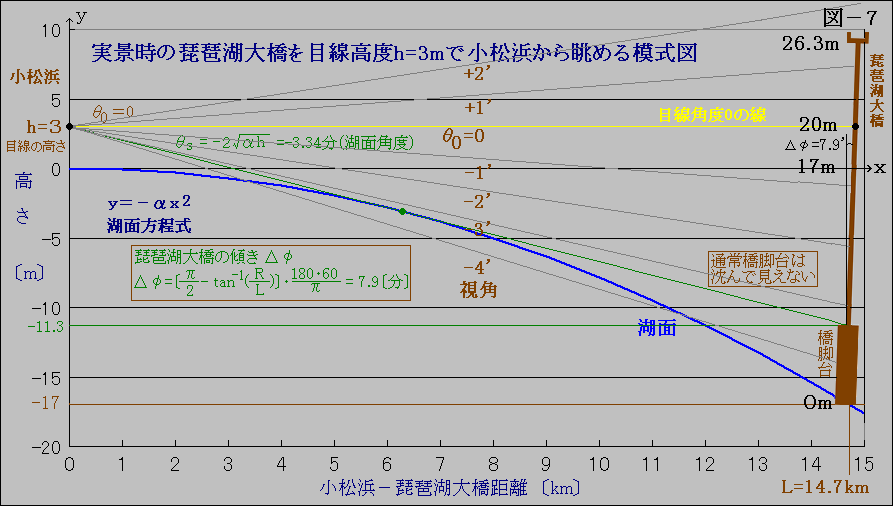
8.シミュレーションに必要な琵琶湖大橋実景画像の準備と解析
実景時の琵琶湖大橋の観察模式図
実景写真から下位蜃気楼をシミュレーションする場合に必要になるのは、実景画像中の分単位の目盛りです。
観測点の視線角度がθ0=0の場合、対象物ではどの高さになるのかを把握することが重要です。
このため、図-7の模式図を作成しました。
琵琶湖大橋(L=14.7km)では、地球の丸さによる落ち込みが17mになり、3mの高さから眺めても橋脚台(フーチング)は沈んで見えません。
目線高度3mを考慮すると、θ0=0の接線は琵琶湖大橋では湖面から20mの高さの所になります。
このことや、
①中央から東西2本目の橋脚間の距離が330mであること(滋賀県道路公社ホームページ)、
②300mmの望遠レンズで撮影した画像では、この間隔が843dot(pixel)であること
③小松浜-琵琶湖大橋間距離がL=14.7kmであること
を用いて、1分=10.9dot(pixel)と結論しました。
これを用いると、中央最も広い橋脚間の距離は140mとなります。視角は32.7分となり太陽や月の視直径とほぼ等しくなります。
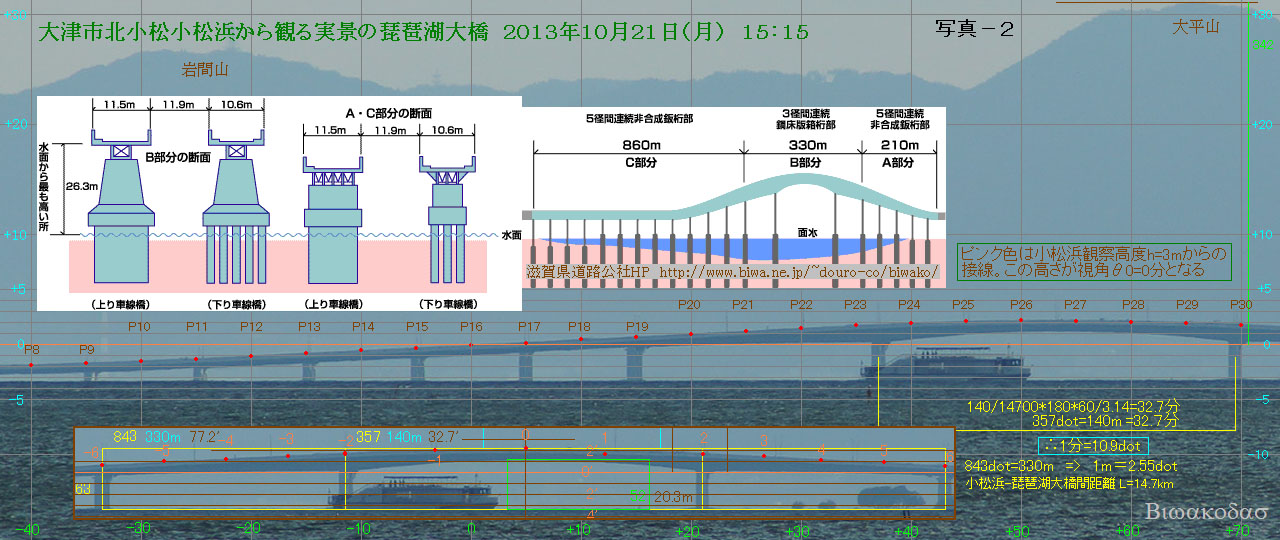
実景時琵琶湖大橋の視線角度を分単位で表示
上の考察に従い、細心の注意を払って写真-2の中に1分単位の視角を水平方向、鉛直方向に記入しました。
図中には、滋賀県道路公社から得た琵琶湖大橋の形状についての画像を貼り付けています。
琵琶湖大橋には、上り(北側)と下り(南側)それぞれ2車線があり、小松浜からは上りの道路がよく見えます。
小松浜視線高度3mからのθ0=0.00〔分〕は、ピンクの横線で示しています。ここは、橋の向こうに聳える大平山の山頂から下へ342dot下った所になります。
大平山は高く、山頂からくる光の下位蜃気楼による曲がりは小さいと考えられるので、この342dot(=31.4分相当)は、下位蜃気楼で全体が下へ落ちている状況でもθ0=0.00〔分〕の位置を確認する重要な決め手となります。
写真の下には、琵琶湖大橋中央部の4つの橋脚が挿入され、B部分(330m)全体が表示できるようにしています。
なお、図中にある赤丸やポイントを識別する記号は、初期段階では蜃気楼曲線に基づいてポイントの移動で下位蜃気楼変化を捉えるために必要としていた名残であり、プログラムで直接実景画像から下位蜃気楼画像への描画に成功したため現在は用いていません。
9.下位蜃気楼シミュレーション手順
手順のまとめ
下位蜃気楼シミュレーションの手順を手短にまとめます。
①地球の丸さを考慮する。ここでは湖面方程式を用いた。
②大気の気温分布t(x,y)のモデルを設定する。ここではt1,t2,dのパラメータでモデル化を行った。
③大気の屈折率の空間分布n(x,y)を設定する。ここでは気温変化を通じてモデル化した。
④光の経路を微小区分に分割し、ホイヘンスの原理を用いて次の区分の光路を定め、初期視角θ0から実景視角θRを得る。
⑤θ0とθRの関係を表す蜃気楼曲線(mirage curve)を作成する。この逆関数を作成すると、下位蜃気楼の物理的意味がよく理解できる。
⑥下位蜃気楼シミュレーションを行いたい実景の画像を用意し、その中に観測点から観た時の視角を1分単位で目盛として位置づける。
今回の計算モデルでは、水平方向(横方向)は一様と考え、鉛直方向の蜃気楼曲線(mirage curve)のみ作成した。
⑦蜃気楼曲線(mirage curve)に基づき、θ0に対応する実景画像の縦1dotの線画像を、θRに対応する位置へ縦1dotだけコピー・ペーストする。
⑧この作業は、θ0=-6分から始め(ただし下位蜃気楼時湖面角θsf以上)、0.05分刻みで+10分まで320回コピー・ペーストの画像処理を繰り返す。
⑨一連の作業を終えると、実景画像は下位蜃気楼画像に変化する。
⑩⑤の過程の中で、折畳線(fold line)視角θfや下位蜃気楼時の湖面視角θsfを決めることができるので、⑧の過程の最後に画像中に線で描画する。
θfは、蜃気楼曲線(mirage curve)の極小値θ0に対応する。θsfは、光の経路計算で湖面にぶつかる絶対値が最小の角となる。
⑪実際の下位蜃気楼画像と比較し、実際と良く合うパラメータ値(t1,t2,d)を見つけて、その物理的意味を吟味する。
これらを実行するに当たり、WindowsXPのパソコンにインストールしたVisualBasic2008を用い、計算は倍精度で行いました。
初期段階では、Excelのシートでシミュレーションテストを行いました。
10.観測画像との比較とパラメータ値
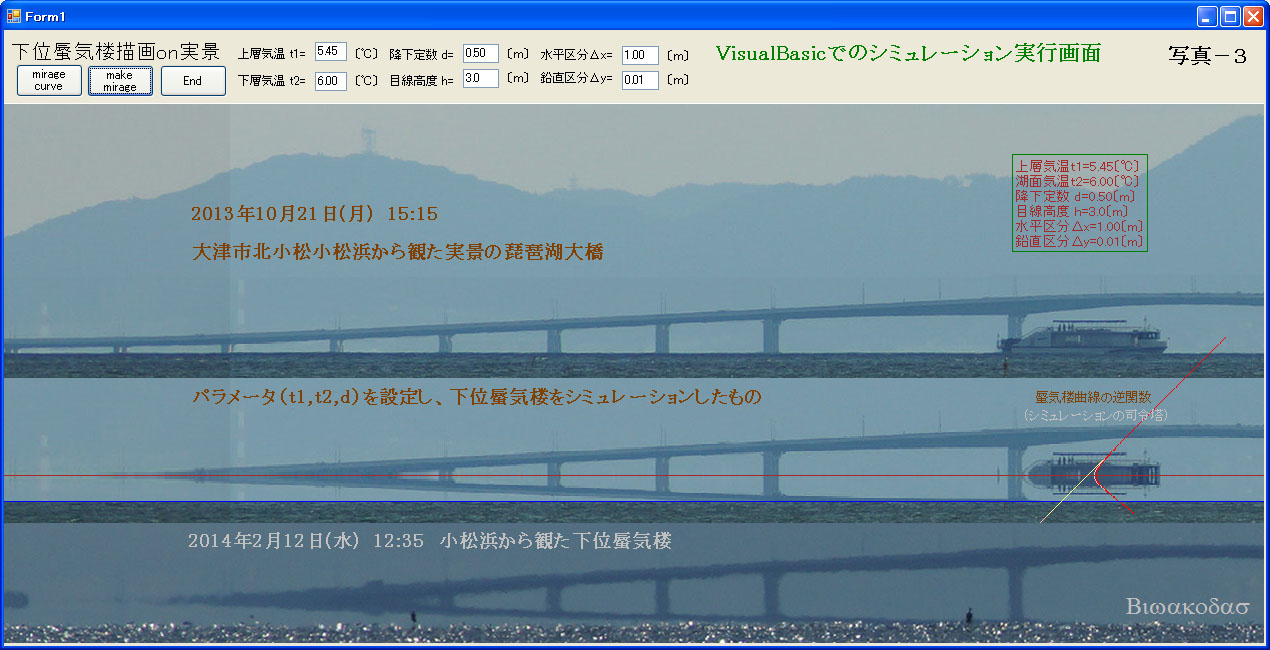
前章の手順でシミュレーションした結果を写真-3に示します。ここでは、t1=5.45℃、t2=6.00℃、d=0.50mを用いました。
実際とよく似た画像が得られますが、実景から作成した下位蜃気楼は、やはり単なる人工的な創作物に見えます。
実際の下位蜃気楼には大気のゆらぎがあり、湖面が近くにきて下がり、表面を揺らぐ波が生き生きと見えます。
シミュレーション画像でも湖面の低下は起きますが、湖面から下は実景の画像がそのまま残っているだけなので、臨場感に乏しくなっています。
臨場感を出すことも今後の課題と言えますが、なかなか難しいと思えます。
ところで、大枠で実際の下位蜃気楼画像に一致したパラメータの設定値:t1=5.45℃、t2=6.00℃、d=0.50mについて吟味してみましょう。
驚くことは、気温の差が湖面と上空で0.55℃しかなく、降下定数は0.50mということです。
大きな波が生じている時にも下位蜃気楼は見た目には変わりなく存在することを考えると、この程度が妥当かなと思えます。
図-5は、最も経路が湖面に近づくのは3.5km程度であることを示しています。
パラメータを変えて日々の下位蜃気楼にフィットする値から、下位蜃気楼の真実に迫れたらと思います。
ここではh=3.0mと固定しましたが、目線の高さhを変えることにより、観察結果を説明するシミュレーションができるかも今後吟味したいと考えています。
11.今後の課題
下位蜃気楼シミュレーションについて、ここ2月で到達した手順について説明をしてきましたが、分かりにくい点も多かろうと思います。
VisualBasicのプログラムを示さないで、手順や結果のみを解説してきたので、具体的に示して欲しいという方もおられることと思います。
プログラムは、いずれかの段階で公表したいと考えています。
さて、ここでの下位蜃気楼シミュレーションは、今後もいろいろな場合の蜃気楼研究に応用できると思います。
下位蜃気楼がある程度解明できた後は、上位蜃気楼の解明に進みたいと思います。
上位蜃気楼の場合には、気温モデルの設定が最も難しいのではと考えています。
直後にこの方法を上位蜃気楼に適応し実り多き成果を得ています。(2014.3.11記)
このホームページは、研究に進展があった時に、順次書き換えて行きたいと考えています。
ご支援、ご教示、アドバイスよろしくお願いします。
前に戻る










