-- 初等幾何学による空気2重層モデルを用いた下位蜃気楼生成線一定の法則の証明 --
琵琶湖地域環境教育研究会 松井 一幸 2001.10.7.
下位蜃気楼では水平線の上に景色が浮くような形になります。そしてある線で折り返すようにこの下に景色が逆さまになって現れます。例えば顕著な例としては北小松で観測した2001年9月22日(土)などが上げられます。
これは以下のように説明できます。半径Rの地球の湖面に暖かい空気層があり、その上に冷たい空気層が乗っていると考えます。暖かい層の厚みをdとしましよう。季節風などにより急に冷たい空気が押し寄せた時、湖面の空気は湖水の暖かい影響を受けて上冷下暖の空気層がよく実現します。実際は暖かい空気層から冷たい空気層への変化は徐々に起きると考えられますが、ここでは簡単の為に空気2重層をモデルとして採用します。
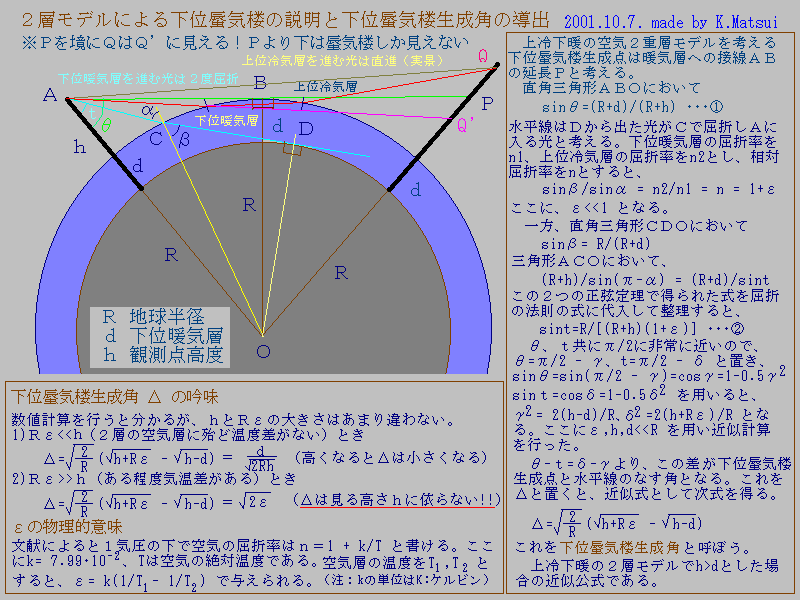
Aから対象物を見る場合、P-B-Aと進んできた光は直進すると考えられます。対象物のPより低い所から出た光はAには届かなくなり、逆に上のQからやってきた光が2回屈折してAに達し、見かけのQ’から来たようにAには写ります。Pより上が倒立した像となって下に移るのですね。ですから琵琶湖大橋を見るときは、レンズ状に見えることになります。
この上下の折り返し線をここでは下位蜃気楼生成線と呼ぶことにします。APとAOのなす角をθとします。一方その下には水平線が存在します。これはDから出た接線がCで屈折してAに入る光をACの方向からやってくると観測します。これをtとします。水平線と下位蜃気楼生成線とのなす角はθ-tで与えられます。これをΔとしましよう。白鬚神社前石段での詳細な観測は、Δ=一定であることを教えています。これを下位蜃気楼生成線一定の法則と呼びました。
正弦定理や近似計算を用いると、図中にあるような計算を経て、下位蜃気楼生成角Δ=θ-t=γ-δについて
Δ=√[2/R](√[h+Rε]-√[h-d])
を算出しました。
1)Rε<<h(温度差が小さいとき)のケースにおいて、Δ=d/√[2Rh]となり、見る高さhの平方根に反比例するという依存性を得ました。
2)Rε>>h(温度差が大きいとき)のケースにおいて、Δ=√[2ε]となり、見る高さや暖気層の厚さには依らない結果を得ました。ε=k(1/T1 - 1/T2)で、空気の屈折率の差からくる因子です。
さて、2)の場合として下位蜃気楼生成線一定の法則を説明しきれるかどうかを吟味する必要があります。この考察は次回に回すことにします。今日はここまでとします。次回をお楽しみに!
前に戻る

